在以太坊数据结构中,Merkle Patricia Trie始终是个绕不过去的坎,世界状态,交易,交易收据等都是以这种树的形式存储在区块链数据库中,并将树root hash保存在区块头里。可以说不弄懂这种树的原理就没有办法真正明白以太坊的数据存储方式。
大家都知道在以太坊cpp版本和go版本采用的是
levelDb这种数据库,这种数据库存储的是[key, value]对。而实际上以太坊存储的数据结构也是[key, value]对,以状态state为例,key是address,value是[nonce, balance, storageRoot, codeHash]。那么问题来了,以太坊为什么不直接按[key, value来存储数据,而要费那么大劲用树型结构来存储呢?
答案是为了安全性。
而为了引进Merkle Patricia Trie,我们要先来看一种简单的树。
Radix Trees
中文翻译为前缀树,这是一种用来查询的数据结构。每次遍历key的一个字符,直到找到对应的值。
比如有下面几个数据:('do', 'verb'), ('dog', 'puppy'), ('doge', 'coin'), ('horse', 'stallion'),存储在Radix Trees里是这样的: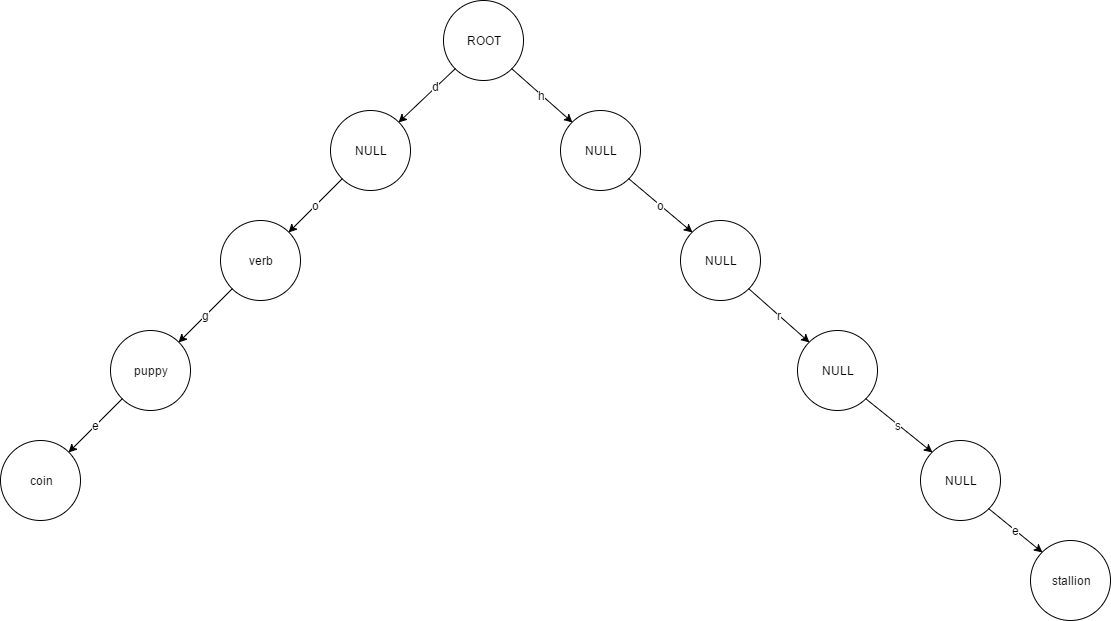
其中圆圈里是值,key的字符组成查询路径,路径是doge时的查询过程为d->o->g->e,需要查询4次,而路径为horse时查询需要5次,因此这种树查询虽然可行,但是效率不高。我们后面可以看到以太坊是怎么解决这个问题的。
解决了查询,然后为了安全性,我们引入了Merkle Trees。
Merkle Trees
Merkle Trees又名Hash Trees,数据都存储在叶节点,父节点则存储叶节点的hash值,一级一级向上, 直到根节点。因此如果修改了叶节点的数据,则父节点hash值就会改变,根节点hash值也会改变,从而很快就可以验证数据是否正确。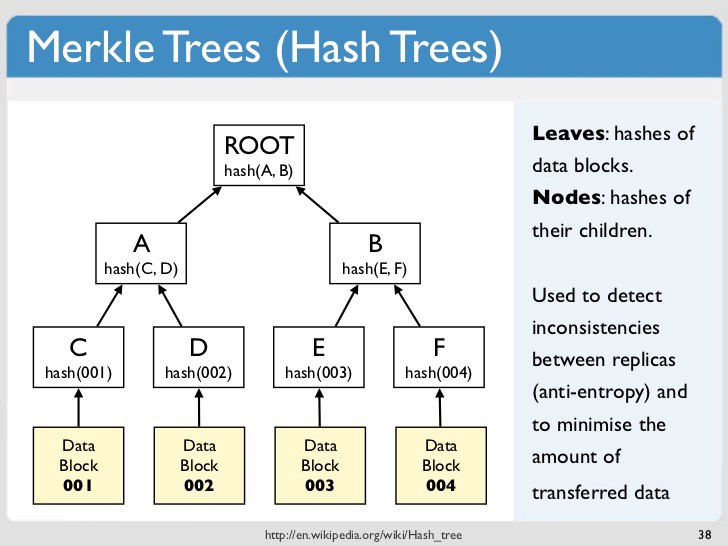
保证数据不被篡改,这是区块链技术的基础。
Merkle Patricia Trie
以太坊Merkle Patricia Trie是结合了上面两种树的数据结构,兼顾了查询和安全性。
查询
前面不是说过Radix Trees查询效率不行吗?那就进行优化,将路径里相同部分提取出来,作为共同路径,从而减少树的高度,提供查询效率。
还是用上面的例子,合并路径后的树变为: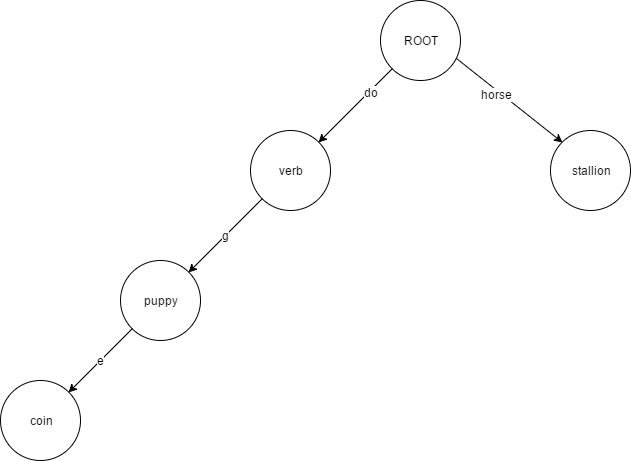
可以看到将do和horse作为共同路径后,查询doge的路径变成了do->g->e,只需要查询3次,而horse只需要查询一次就够了。
安全性
节点与节点之间的联系不再采用内存指针的方式,而是采用hash值的方式,比如上图中的puppy这个值的节点存储执行下一个节点的hash值,然后将这个hash值与实际节点对应关系存储在[key, value]的数据库中。当有人篡改coin节点值时,也必须要修改puppy节点里的hash值,然后verb节点里hash值也需要修改,直到根节点,所以我们只需要验证根节点的hash值,就知道底层数据是否正确。
节点类型
按功能不同,存在4种节点:
- NULL节点
- 分支节点,含有17项数据,[ v0 … v15, vt ]
- 叶节点,含有2项数据,[ encodedPath, value ]
- 扩展节点,含有两项数据,[ encodedPath, key ]
Merkle Patricia Trie查询路径是以nibble(半个字节)作为单位。
分支节点中的前16项数据v0-v15分别对应16进制的0-0xF,是用nibble作为索引,可以快速进行查询,比如路径nibble是0xa,则取分支节点0xa位置的值。分支节点对应图上的分叉节点。
叶节点和扩展节点都是两项,只是value不同,那么怎么区分他们呢?
以太坊是采用添加前缀的方式,根据节点类型和路径长度是否是奇偶数来添加不同的前缀。
有一个对应表:
| hex char | bits | node type partial | path length |
|---|---|---|---|
| 0 | 0000 | extension | even(偶数) |
| 1 | 0001 | extension | odd(奇数) |
| 2 | 0010 | terminating (leaf) | even(偶数) |
| 3 | 0011 | terminating (leaf) | odd(奇数) |
可以看到前缀为0或者1时表示扩展节点,2或者3时表示叶节点。
另外前缀为0或者2时,需要变更为00或20.
例子1
我们用一个例子来说明: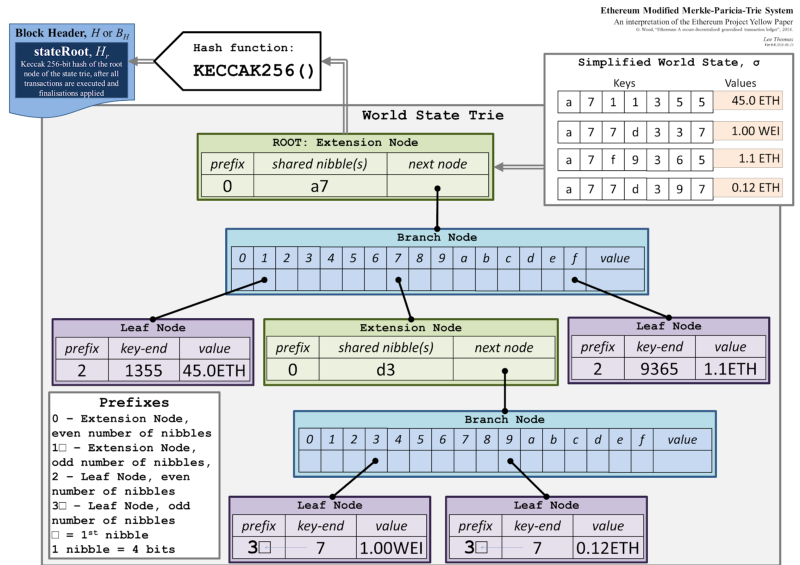
图中右上角有4个[key, value]对,我们要存储这4对数据。key每个方框里是一个nibble。
- 从这四个路径中可以提取出公共路径
a7,因此可以建立一个扩展节点A, [00 a7, hashB],a7是一个偶数长度的扩展节点,前缀为00,hashB是下一个节点B的hash值。 - 下一个
nibble取值有1, 7, f,因此节点B为一个分支节点,其中index为1,7,f的位置保存下一个节点的hash值,value为空。这个分支节点为:[ EMPTY, hashC, EMPTY, EMPTY, EMPTY, EMPTY, EMPTY, hashD, EMPTY, EMPTY, EMPTY, EMPTY, EMPTY, EMPTY, EMPTY, hashE, value]。hashC, hashD, hashE为下一层节点的hash值 - 因为出现了分支,我们来看1这个分支,这个分支后没有分支,所以后续的1355可以作为一个叶节点,为[20 1355, 45.0ETH],这里1355为偶数长度的叶节点,所以前缀为20。
- 再来看7这个分支,后续又有d3这共同路径,因此创建一个扩展节点D,[00 d3, hashF],’d3’是一个偶数长度的扩展节点,前缀为00,
hashF是下一个节点F的hash值。 d3之后又出现分支3和9,因此又出现一个分支节点,其中index为3和9的位置保存下一个节点的hash值,value为空。这个节点为:[ EMPTY, EMPTY, EMPTY, hashG, EMPTY, EMPTY, EMPTY, EMPTY, EMPTY, hashH, EMPTY, EMPTY, EMPTY, EMPTY, EMPTY, EMPTY, value]- 剩下的就是两个叶节点,分别为[37, 1.00WEI]和[37, 0.12ETH],这两个都是奇数长度的叶节点,因此前缀为3。
- 其他节点可以按同样的方法分析。
例子2
我们再用前面的('do', 'verb'), ('dog', 'puppy'), ('doge', 'coin'), ('horse', 'stallion')做例子来说明分析过程。
由于是采用nibble作为路径单位,所以先将路径和值都写为字节形式:
1 | <64 6f> : 'verb' |
那么在数据库中存储形式为:
1 | rootHash: [ <16>, hashA ] |
我们来模拟一下真实的查询过程,假如我们要查询doge这个key对应的值是多少。
rootHash已知(存储在区块头中),那么从levelDb中读出key为rootHash的值,也就是[ <16>, hashA ],这是一个扩展节点,路径为6,剩下路径为4,6,f,6,7,6,5,并得到下一个节点hashA- 在
levelDb中读出key为hashA的值,也就是 [ <>, <>, <>, <>, hashB, <>, <>, <>, hashC, <>, <>, <>, <>, <>, <>, <>, <> ],nibble为4,在位置4读出下一个节点hashB,剩余路径为6,f,6,7,6,5 - 在
levelDb中读出key为hashB的值,也就是[ <00 6f>, hashD ],这是一个路径为6f的扩展节点,因此剩余路径为6,7,6,5,并得到下一个节点hashD - 在
levelDb中读出key为hashD的值,也就是 [ <>, <>, <>, <>, <>, <>, hashE, <>, <>, <>, <>, <>, <>, <>, <>, <>, ‘verb’ ],nibble为6,在位置6读出下一个节点hashE,剩余路径为7,6,5 - 在
levelDb中读出key为hashE的值,也就是 [ <17>, hashF ],这是一个路径为7的扩展节点,因此剩余路径为65,并得到下一个节点hashF - 在
levelDb中读出key为hashF的值,也就是[ <>, <>, <>, <>, <>, <>, hashG, <>, <>, <>, <>, <>, <>, <>, <>, <>, ‘puppy’ ],nibble为6,在位置6读出下一个节点hashG,剩余路径为5 - 在
levelDb中读出key为hashG的值,也就是[ <35>, ‘coin’ ],这是一个路径为5的叶节点,正好和我们的剩余路径吻合,因此我们就得到了最终的值coin。
可见以太坊为了安全性真的增加了不少复杂性,降低了效率。
以太坊中的应用
以太坊中实际情况还要复杂,数据还需要通过RLP编码。
- State Trie(世界状态树)
路径是sha3(ethereumAddress),value是rlp([nonce,balance,storageRoot,codeHash]) - Transactions Trie(交易树)
路径是rlp(transactionIndex),value是rlp(transaction) - Receipts Trie(交易收据树)
路径是rlp(transactionIndex),value是rlp(transaction receipt)
参考
Understanding Trie Databases in Ethereum
Modified Merkle Patricia Trie Specification (also Merkle Patricia Tree)

